Boolean algebra rules is important rule in digital electronics. It is a type of algebra that deals with the binary variable data. The binary variable data is “zero” and “one”. The basic operation of Boolean algebra is AND and OR operations. The Boolean algebra rules use the binary number and these binary no’s is “0” and “1”.
For instance, consider the Boolean function:
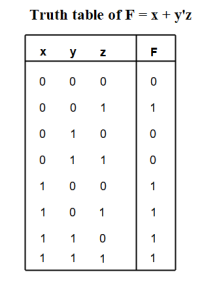
F = x + y’z
The logic diagram for this is F = x + y’z represented as:

Boolean algebra logic diagram
- The Boolean F = x + y’z function is converted from an algebraic expression to a logical diagram AND, OR, and NOT gates.
- Inverter input ‘y’ generates its y’ complement.
- The AND gate operation for the term y’z, and OR gate operation is used for combine the two terms (x and y’z).
- The function variable is considered a circuit input, and the variable function is considered to be a circuit breaker.
The truth table for the Boolean function F = x + y’z can be represented as:
What Does Boolean algebra rules?
Boolean algebra is a type of mathematical function, unlike the common algebra, which works with binary digits “0” and “1”. Although 1 represents truth or high, 0 represents false or low. Computers can perform complex tasks via using Boolean function. Boolean algebra and Boolean functions is a basic language of computer system or networking.
Unlike standard mathematical operations – addition, subtraction, multiplication and division – performance in Boolean algebra is unique and limited in number. There are three Boolean functions whose are AND, OR and NOT. The function NOT opposite is the reverse value of the given input signal. For example, 0 is the opposite of 1 and vice versa. AND operation returns 1 in case both inputs equal to 1 otherwise result is zero. Function OR returns only 1 if one of the given values is 1. If not, it returns the value of 0.
The Boolean algebra was named after George Boole, a mathematician who first described it in 1847.
Boolean algebra Rules
Since Boolean algebra is widely used in the digital computer and digital electronics engineering to simplifying logic circuits and doing this, there are some rules to follow. The Boolean algebra has only two value these are “0” and “1”. The some rules of Boolean algebra are briefly described below:
Some basic logical Boolean operations,
AND Operation
0.0=0
0.1=0
1.0=0
1.1=1
OR Operation
0+0=0
0+1=1
1+0=1
1+1=1
Not Operation
1’=0
0’=1
Laws of Boolean Algebra rules
- 1’=0, 0’=1, A=1 if A’=0 and A=0 if A’=1
- A . 0 →0, where A can be either 0 or 1.
- A . 1 →A, where A can be either 0 or 1.
- A . A →A, where A can be either 0 or 1.
- A . Ā →0 , where A can be either 0 or 1.
- A + 0 →A , where A can be either 0 or 1.
- A + 1 →1, where A can be either 0 or 1.
- A + Ā →1,
- A + A →A,
- A + B →B + A, where A and B is possible to 0 or 1.
- A . B →B . A, where A and B is possible to 0 or 1.
These laws of Boolean algebra are same for the more than three inputs.
Cumulative Law for Boolean algebra
A + B + C = A+C+ B = B + C+ A
A . B . C = A . C . B = B . C. A
According to Cumulative Law, the order of AND operations and OR operations conducted.
Associative Laws for Boolean Algebra
This law has many inputs variables, where the OR operation of the variables result is the sum of variables. This law AND operation is same as of multiplication.
A+(B+C) = (A+B)+C
A.(B.C) = (A.B).C
Distributive Laws for Boolean Algebra
This law is mixture of two operators, that operations are AND and OR.
A.(B+C) = (A.B)+(A.C)
A+(B.C) = (A+B).(A+C)
Redundant Literal Boolean Algebra Rules
AA+A’A+AB+A’B
From the truth table,
| Inputs | Output | ||
| A | B | ĀB | A + ĀB |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 |
| Inputs | Output | |
| A | B | A+B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
From the truth table,
A+A’B=A+B
Similarly
A(A’+B) = AB
Absorption Laws for Boolean algebra
A+AB = A
from truth table,
| Inputs | Output | ||
| A | B | AB | A+A.B |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Input A and output A(A+B) column is the same.
From truth table,
| A | B | A+B | A.(A+B) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
Annulment law
A variable AND with 0 gives 0, while a variable OR with 1 gives 1.
A.0 = 0
A + 1 = 1
Identity law
In this law variable remain unchanged it is OR with ‘0’ or ANDwith ‘1’.
A.1 = A
A + 0 = A
Idempotent law
A variable not change when it is ANDed or ORed with itself.
A + A = A
A.A = A
Complement law
In this Law if a complement is added to a other input it gives one, if a variable is multiplied with its complement the results is ‘0’.
A + A’ = 1
A.A’ = 0
Double negation law
A variable with two compliments its symbol gets cancelled out and original variable is obtained.
((A)’)’=A
Absorption law
This law involved absorbs similar input.
A + AB = A
De Morgan law
The operation of an AND or OR logic circuit is change when all inputs are inverted.
(A.B)’ = A’ + B’
(A+B)’ = A’.B’
Applications of Boolean algebra rules
The use of Boolean algebra can be in any domain where the variables have two dimensions. Some real-life applications of Boolean algebra are given below.
- Automatic dining machine that produces coffee, milk or tea. Here the whole drink is presented with two exceptions (‘1’) or non-extraction (‘0’). The output is a selection of any of those three options.
- In the use of a U.S. rocker launcher, the concept behind the Boolean algebra is used. It has a presidential button and three advisor buttons, and these are considered ideas. The output is ‘1’ (missile fire) if the conditions below are true
Other applications include a two-story elevator, counters, clocks, seven-component displays, digital clocks, electronic circuitry, and many more.
Therefore, we conclude that Boolean numbers are completely different from real numbers and are a different kind of numbers. Due to its wide use and use, Boolean algebra is very prominent. So, do you know how Boolean Algebraic expressions are used?